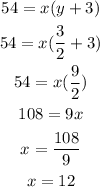ANSWER :
Jeff's speed is 12 mph
EXPLANATION :
The football game is 54 miles from their apartment.
Ian drives 24 mph faster than Jeff,
so if Jeff's speed is x,
Ian's speed will be x + 24
It takes 3 hours longer than Ian to get to the game,
so if Ian takes y hours to get to the game,
Jeff's time will be y + 3
Recall the equation of speed, time and distance.
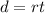
where d = distance
r = speed
t = time
Equation for Jeff :

Equation for Ian :
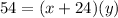
Express Jeff's equation as x in terms of y.
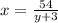
Substitute this to Ian's equation :
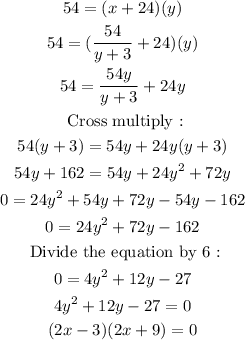
Equate the factors to 0.
2x - 3 = 0
2x = 3
x = 3/2
2x + 9 = 0
2x = -9
x = -9/2
Note that there's no negative time, so we will consider x = 3/2 only
Substitute x = 3/2 to Jeff's equation :