Question

Instructions: Determine which of the points given are in the solution area for the system of inequalities

Answer 1

Given the following inequalitites:

`\begin{gathered} y\leq(1)/(2)x+2 \\ y\ge-2 \\ x\leq-3 \end{gathered}`

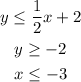
We are going to evaluate each point:

A= (-10 , 1)

B= (-3, 7 )

C= ( 5 , 1)

D= (-3 , -5)

The point A:

`\begin{gathered} 1\leqslant(1)/(2)(-10)+2=1\leqslant-5+2=1\leqslant-3 \\ \end{gathered}`

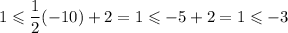
As -3 is not greater or equal to 1 the point A does not work.

Point B:

`7\leqslant(1)/(2)(-3)+2=7\leqslant-(3)/(2)+2=7\leqslant(1)/(2)`

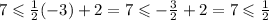
1/2 is not greater or equal to seven, the point B does not work.

Point C.

`1\leqslant(1)/(2)(5)+2=1\leqslant(5)/(2)+2=1\leqslant(9)/(2)`

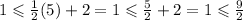
9/2 is greater than 1, now we have to evaluate the other inequalities in the same point.

`\begin{gathered} 1\ge-2 \\ and \\ 1\leq-3 \end{gathered}`

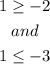
As -3 isn't greater than 1, the point c does not work.

The point D.

`-3\leqslant(1)/(2)(-5)+2=-3\leqslant-(1)/(2)`

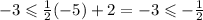
The first one is true, -1/2 is greater than -3.

`-5\ge-2`

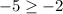
The second one is false, the point D does not work.

Point E (0 , 0).

`0\leqslant(1)/(2)(0)+2=0\leq2`

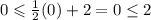
The first is true.

Second one:

`0\ge-2`

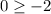
The second one is true.

Third one.

`0\leq-3`

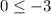
The point E does not work, because -3 is not greater or equal to -3.

Answer: no point is a solution of the system.