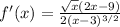ANSWER
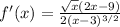
Step-by-step explanation
Before finding the derivative of this function, we can simplify it. This will also simplify the process of derivation.
We include x inside the square root if we square it, and the same for the denominator (x - 3),
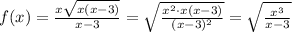
Now we apply the chain rule,
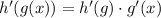
In this case, h(g) is the function f and g(x) is the expression inside the square root,
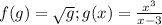
Let's find the derivative of f(g). Remember that the square root can be written as a power with exponent 1/2,
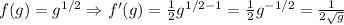
Then, find the derivative of g(x). To do so, we have to apply the quotient rule,
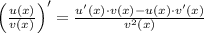
In this case, u(x) = x³ and v(x) = x - 3. Let's find the derivative of each and the square of v(x),
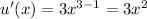
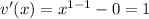
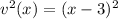
So, the derivative of g(x) is,
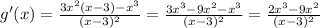
Finally, plug in g'(x) and f'(g(x)) in the chain rule expression we found above,
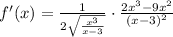
This expression can be simplified. First, distribute the square root of the first factor and rewrite it using fractional exponents,
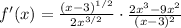
Simplify the exponents of the factor (x - 3),
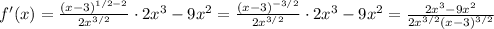
We can also take x² as a common factor in the numerator to simplify that with the denominator,
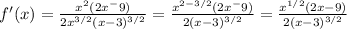
Hence, the derivative of the function is,