Question

Which of the following is not a valid way ofstarting the process of factoring60x2 + 84x + 49?Choose the inappropriate beginning below.O A. (X (60)OB. (2x (30)O C. (6x (10x)OD. (2x (5x)

Answer 1

When we do the distributive, in the correct way, we must find 60x² on the first term. Therefore, let's multiply the terms on all options and see which one does not result in 60x².

Let's do the letter A first, we have

`(x\text{ })(60x\text{ })`

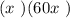
When we do the distributive we would have

`x\cdot60x=60x^2`

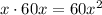
As we wanted, then the letter A is appropriate. If the letter A is appropriate, let's test letter B

`\begin{gathered} (2x\text{ })(30\text{ }) \\ \\ 2x\cdot30x=60x^2 \end{gathered}`

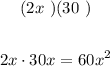
As we expected.

For the letter C, we will have

`\begin{gathered} (6x\text{ })(10x\text{ }) \\ \\ 6x\cdot10x=60x^2 \end{gathered}`

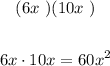
Now the last one is the letter D.

`\begin{gathered} (2x\text{ })(5x\text{ }) \\ \\ 2x\cdot5x=10x^2 \end{gathered}`

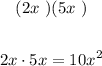
That's not appropriate, the correct would be 60x², therefore, the inappropriate beginning is the letter D.