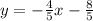Answer:
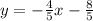
First, let us find the slope of the line using the following equation:
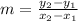
Using the points (3, -4) and (8, -8)
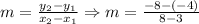
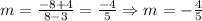
Now that we found the slope of the line, we are going to use the following equation to solve for the equation of the line:
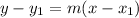
Using the point (3, -4)
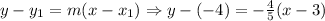
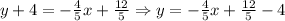
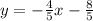
Therefore, the equation of the line that passes through the points (3, -4) and (8, -8) is: