Question

Out of 300 people sampled, 111 preferred Candidate A. Round to three decimals.Based on this estimate, what proportion (as a decimal) of the voting population (p) prefers Candidate A?Compute a 90% confidence interval, and give your answers to 3 decimal places.

Answer 1

We are given that out of 300 people, 111 preferred candidate A. The proportion that prefer candidate A is the number of people that prefer candidate A divided by the total population, like this:

`P=(111)/(300)`

Solving the operation:

`P=0.37`

Therefore, the proportion that prefers candidate A is 0.37.

To determine the confidence interval we use the following formula:

`CI=(P-z\sqrt{(P(1-P))/(n)},P+z\sqrt{(P(1-P))/(n)})`

Where:

`\begin{gathered} P=\text{ proportion} \\ n=\text{ size of the population} \\ z=\text{ critical value} \end{gathered}`

The critical value for a 90% confidence interval is:

`z=1.64`

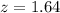
Now, we substitute the values in the formula:

`CI=(0.37-1.64\sqrt{((0.37)(1-0.37))/(300)},0.37+1.64\sqrt{((0.37)(1-0.37))/(300)})`

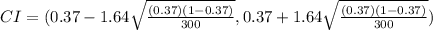
Solving the operations:

`CI=(0.324,0.416)`

And thus we get a confidence interval of 90% confidence.