Question

Do you know how to solve a system using a matrix, and explain clearly how to do that? 4x - 12y = -16x + 4y = 4

Answer 1

`\begin{gathered} 4x-12=-1 \\ 6x+4y=4 \end{gathered}`

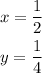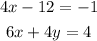
We want to solve this system using a matrix.

The first step is write a matrix whose each line will correspond to a equation and each term will correspond to a coeficient. The terms of the firs colum will correspond to the coeficients of x, the terms of the second colum will correspond to the coeficients of y and the terms of the third colum will correspond to the independent term in the right side of the equation:

`\begin{bmatrix}{4} & {-12} & {-1} \\ {6} & {4} & {4} \\ {\square} & {\square} & {\square}\end{bmatrix}`

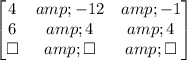
Now, we must conduct operations to escalonate the terms corresponding to the coefficients multiplying x and y

First, we multiply the second line by 3:

`\begin{bmatrix}{4} & {-12} & {-1} \\ {18} & {12} & {12} \\ {\square} & {\square} & {\square}\end{bmatrix}`

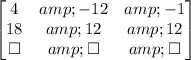
Then, we add line 2 to line 1:

`\begin{bmatrix}{22} & {0} & {11} \\ {18} & {12} & {12} \\ {\square} & {\square} & {\square}\end{bmatrix}`

Now, we divide line 1 by 22

`\begin{bmatrix}{1} & {0} & {(1)/(2)} \\ {18} & {12} & {12} \\ {\square} & {\square} & {\square}\end{bmatrix}`

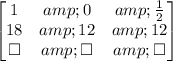
Then, we subtract 18 times line 1 from line 2:

`\begin{gathered} \begin{bmatrix}{1} & {0} & {(1)/(2)} \\ {18-18} & {12} & {12-(18)/(2)} \\ {\square} & {\square} & {\square}\end{bmatrix} \\ \begin{bmatrix}{1} & 0 & {(1)/(2)} \\ {0} & {12} & {3} \\ {\square} & {\square} & {\square}\end{bmatrix} \end{gathered}`

Now, we divide line 2 by 12:

`\begin{bmatrix}{1} & {0} & {(1)/(2)} \\ {0} & {1} & {(1)/(4)} \\ {\square} & {\square} & {\square}\end{bmatrix}`

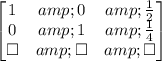
Finally, we can rewrite these terms in the form of equations and obtain the solution:

`\begin{gathered} x=(1)/(2) \\ y=(1)/(4) \end{gathered}`