The optimal lenght of x and y are:
x = 30ft
y = 30ft
To solve this, we want to know the best lenght of x and y to get the maximum area.
Then, we know the perimeter of the pens: 120ft
The perimeter is the sum of all the sides:
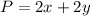
Sinnce we have 2 sides of lenght x and 2 sides of length y
Also, we know how the area is calculated. Base times height:
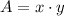
Now, we know the perimeter he has is 120ft. Then, we can replace P = 120ft and solve for y:

Now we can replace y in the area equation:
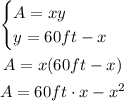
Here we have a function of the area respect x.
Then, we want to find the maximum area possible. We know that the zeroes of the derivative of a function is where we can find maximums and minimums.
Then let's derivate the function of the area:
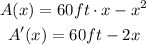
Now let's find the zero of the derivative:
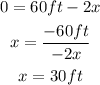
This is the value of x that maximizes the area with a perimeter of 120ft.
Now let's find the value of y:
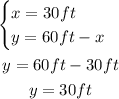
Then the maximum area is with a lenght of y = 30ft and x = 30ft.
This also tell us that the shape that maximizes the area of a 4 sided shape with a certain perimeter is a square.