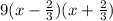To find the factored form of a polynomial, like:
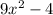
We can start by finding its zeros.
This is a quadratic equation, so if both of its zeros are real, we can rewrite it as:
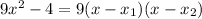
To find the zeros, x₁ and x₂, we can equalize the polynomial to zero and solve for x:
![\begin{gathered} 9x^2-4=0 \\ 9x^2=4 \\ x^2=(4)/(9) \\ x=\pm\sqrt[]{(4)/(9)} \\ x=\pm\frac{\sqrt[]{4}}{\sqrt[]{9}} \\ x=\pm(2)/(3) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/5fsmxalm4pkpmd2pvi94p05xhi4346q78q.png)
So, the roots are +2/3 and -2/3.
The factored form is, then:
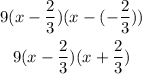
Answer: The factored form is: