Question

if you divide a number by a fraction less than 1, is the result larger or smaller than the original number? Explain.

Answer 1

Question:

if you divide a number by a fraction less than 1, is the result larger or smaller than the original number? Explain.

Concept:

We will solve the question using an example below

Let us consider the number which is the numerator as(original number)

`n=4`

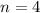
Let us consider a fraction less than 1 below as

`f=(1)/(4)`

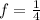
Then we will divide the number by a fraction less than 1,

`(n)/(f)`

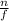
By substituting the values , we will have

`\begin{gathered} (n)/(f) \\ =(4)/((1)/(4)) \\ by\text{ applying the relation below, we will have} \\ a/(1)/(b)=a*(b)/(1)=ab \\ (4)/((1)/(4))=4/(1)/(4)=4*(4)/(1)=16 \end{gathered}`

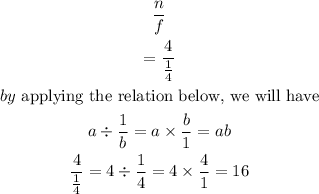
Hence,

If you divide a number by a fraction less than 1, is the result LARGER THAN THE ORIGINAL NUMBER