Assuming the bubble as an idel gas, we use the following
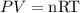
Where the pressure at sea level is 101K Pa.
The pressure would be given by
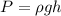
Whew rho = 1000 kg/m^3, g = 9.8 m/s^2, and h = 18m.
![\begin{gathered} P=\frac{1000\operatorname{km}}{m^3}\cdot(9.8m)/(s^2)\cdot18m \\ P_{\text{under}}=176,400Pa+101,000Pa=277,400Pa \\ \end{gathered}]()
The pressure under the water is 277,400 Pa.
Then, form a ratio between the initial condition of the ideal gas and the final conditions.
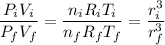
Observe that the radii are not simplified because there's a change. Solve for the final radius.
![\begin{gathered} r^3_f=(P_(under)\cdot r_i3)/(P) \\ r_f=\sqrt[3]{(277,400Pa\cdot r^3_i)/(101,000Pa)}=r_i\sqrt[5]{2.75}=1\operatorname{cm}\cdot1.4 \\ r_f=1.4\operatorname{cm} \end{gathered}]()
Therefore, the answer is c. 1.4 cm.