Question

Lorene plans to make several open-topped boxes in which to carry plants. She makes the boxes from rectangular sheets of cardboard from which she cuts out 4-in squares from each corner. The length of the original piece of cardboard is 8 in more than the width. If the volume of the box is 1232 in, determine the dimensions of the original piece of cardboard.

Answer 1

Notice that the height of the box is equal to 4 in. Therefore, the volume of the box is

`V=l\cdot w\cdot h=(x+8-8)\cdot(x-8)\cdot4=4x(x-8)`

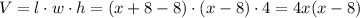
Where l is the length, w is the width, and h is the height of the box.

Therefore, since the volume of the box is 1232 in^2

`\begin{gathered} \Rightarrow1232=4x(x-8) \\ \Rightarrow1232=4x^2-32x \\ \Rightarrow4x^2-32x-1232=0 \\ \Rightarrow x^2-8x-308=0 \end{gathered}`

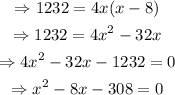
Solve the quadratic equation as shown below,

`\begin{gathered} \Rightarrow x=\frac{8\pm\sqrt[]{64+1232}}{2}=(8\pm36)/(2)\to\text{ x has to be positive because it is a length} \\ \Rightarrow x=22 \end{gathered}`

Thus, the answer is that the original length is equal to 30in and the original width is 22in.