Question

The top says..."here is a system of equations. y=2x+3 y=x-1Graph the systems. Then write its solution. Note that you can also answer "no solution" or "infinitely many" solutions"

Answer 1

To solve an equation system using a graph, you have to draw the lines that correspond to each equation.

• If the lines are parallel, it means that the system has no solution

,

• If both equations lead to the same line, then the system has infinite solutions

,

• If the lines intersect at one point, the said point will be the solution of the system

To graph each line, you have to determine at least two points for each line, plot the points and draw the line.

I will determine the points of both lines using x=-3 and x=3

First equation y=2x+3

For x=-3

`\begin{gathered} y=2x+3 \\ y=2\cdot(-3)+3 \\ y=-6+3 \\ y=-3 \end{gathered}`

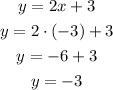
The point coordinates are (-3,-3)

For x=3

`\begin{gathered} y=2x+3 \\ y=2\cdot3+3 \\ y=6+3 \\ y=9 \end{gathered}`

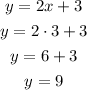
The coordinates of the point are (3,9)

Second equation y=x-1

For x=-3

`\begin{gathered} y=x-1 \\ y=-3-1 \\ y=-4 \end{gathered}`

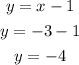
The coordinates are (-3,-4)

For x=3

`\begin{gathered} y=x-1 \\ y=3-1 \\ y=2 \end{gathered}`

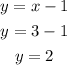
The coordinates are (3,2)

Plot the points for both lines and determine the solution of the system:

The lines intersect at the point (-4,-5), this point is the solution of the equation system.