Question

the demand equation for a certain product is given by p=132-0.025x, where P is the unit price (in dollars) of the product and x is the number of units produced. The total revenue obtained by producing and selling x units is give by R=xpDetermine prices P that would yield a revenue of 7280 dollars.Lowest such price=______dollarsHighest price=______dollars

Answer 1

We have that the demand equation for a certain product is given by:

`P=132-0.025x`

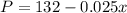
where x is the number of units produced. Also, that the total revenue is:

`R=xP`

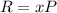
And we want to determine prices P that would yield a revenue of 7280 dollars. This means that we want to find values x such that the following equation holds:

`7280=xP=x(132-0.025x)`

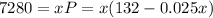
We will solve the equation by the quadratic formula. First, we will use the distributive property and we clear out the left side of the equation, to obtain:

`\begin{gathered} 7280=132x-0.025x^2 \\ 0=132x-0.025x^2-7280 \\ 0=-0.025x^2+132x-7280 \end{gathered}`

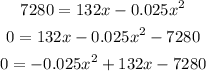
In this equation:

`\begin{gathered} a=-0.025 \\ b=132 \\ c=-7280 \end{gathered}`

And thus, replacing on the quadratic formula we obtain:

`\begin{gathered} x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \\ =\frac{-132\pm\sqrt[]{(132)^2-4(-0.025)(-7280)}}{2(-0.025)} \\ =\frac{-132\pm\sqrt[]{17424-728}}{-0.05} \\ =\frac{-132\pm\sqrt[]{16696}}{-0.05} \\ \approx(-132\pm129.21)/(-0.05) \end{gathered}`

Now, for the two solutions, we separate them with the signs + and -.

`\begin{gathered} x_1=(-132+129.21)/(-0.05) \\ \approx55.8 \end{gathered}`

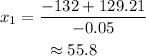
And for the other one:

`\begin{gathered} x_2=(-132-129.21)/(-0.05) \\ \approx5224.2 \end{gathered}`

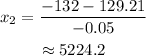
This means that the lowest of the prices should be 56 dollars, and the highest price 5224 dollars.