Question

For each line find the SLOPE between the 2 points given - simply each fraction to prove that the lines have a CONSTANT rate of change :1) Point T : 2) Point R : 3) Point S :4) Slope of TR :5) Slope of RS :6) Slope of TS :7) Describe the SLOPE of the line :8) Therefore the CONSTANT rate of change is ....?

Answer 1

First, find the coordinates of each point looking to the graph.

1) Point T: (-5,0)

2) Point R: (1,2)

3) Point S: (7,4)

Use the slope formula to find the slope for each pair of points:

`\begin{gathered} m_(TR)=(2-0)/(1-(-5)) \\ =(2)/(1+5) \\ =(2)/(6) \\ =(1)/(3) \end{gathered}`
`\begin{gathered} m_(RS)=(4-2)/(7-1) \\ =(2)/(6) \\ =(1)/(3) \end{gathered}`
`\begin{gathered} m_(TS)=(4-0)/(7-(-5)) \\ =(4)/(7+5) \\ =(4)/(12) \\ =(1)/(3) \end{gathered}`

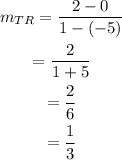
Therefore, the slope of TR, RS and TS is 1/3.

7) The slope of the line is constant and equal to 1/3.

8) The constant rate of change of the line is 1/3.