Question

Line m passes through the points (4, 1) and (7,3) while line n passes through the points (-3, 5) and (-9, 1).Which statement accurately describes the relationship between the twolines?

Answer 1

Given:

Line m passes through the points (4, 1) and (7,3) while line n passes through the points (-3, 5) and (-9, 1).

Required:

Which statement accurately describes the relationship between the two

lines?

Step-by-step explanation:

The slopes of parallel lines are equal.

We know slope between two points

`m=(y_2-y_1)/(x_2-x_1)`

For (4, 1) and (7, 3)

`\begin{gathered} m=(3-1)/(7-4) \\ =(2)/(3) \end{gathered}`

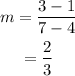
For (-3, 5) and (-9, 1)

`\begin{gathered} m=(1-5)/(-9+3) \\ =(-4)/(-6) \\ =(2)/(3) \end{gathered}`

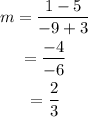
Slopes of both lines m and n is equal.

Answer:

Option A is correct.