Checking each equation one by one.
First, take the equation 5x+5y=10
Now, take 5 commons on both sides of the equation.
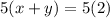
Now, cancel out 5 from both sides of the equation.
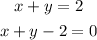
Hence, proved this equation is not equivalent to equation x+y-10=0.
Now, check the second equation.
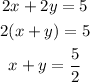
This equation is not equivalent to the equation x+y-10=0.
Now, check the equation third.
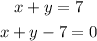
It is clear that this equation is also not equivalent to the equation x+y-10=0.
Now, check the last equation.
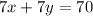
Take the 7 commons from both sides of the equation.
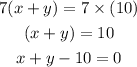
Hence, proved this equation is equivalent to the equation x+y-10=0.
Therefore, the given option 7x+7y=70 is correct.