Question

the triangles are similar. the area of the larger triangle is 1583 ft². Find the area of the smaller triangle to the nearest square foot

Answer 1

223 ft²

Step-by-step explanation:

First, we need to find the scale factor. So, taking into account the lengths of the triangles, we get that the scale factor is:

`k=\frac{15\text{ ft}}{40\text{ ft}}=0.375`

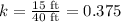
Then, to know the area of the smaller triangle, we will use the following equation:

`A_{2\text{ }}=k^2(A_1)`

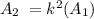
Where A2 is the area of the smaller triangle and A1 is the area of the larger triangle.

So, replacing k by 0.375 and A1 by 1583 ft², we get that the area of the smaller triangle is equal to:

`\begin{gathered} A_2=(0.375)^2(1583) \\ A_2=(0.1406)(1583) \\ A_2=222.6\approx223ft^2 \end{gathered}`

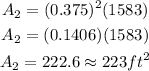
Therefore, the answer is 223 ft²