Question

Graphing a liner equation

Answer 1

The equation of the line we have been asked to plot is:

`y=(2)/(3)x+3`

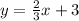
First of all, let us compare this equation to the standard equation of a line. The standard equation is given by:

`\begin{gathered} y=mx+c \\ m=\text{slope} \\ c=y-\text{intercept (the value of y when x = 0)} \end{gathered}`

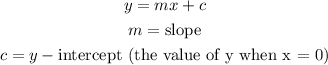
Hence we can conclude that:

`\begin{gathered} \text{slope(m)}=(2)/(3) \\ y-\text{intercept(c)}=3 \end{gathered}`

Whenver the value of the slope is positive as it is in this case, then the graph should move upwards from left to right. i.e. /.

Hence, Option D is wrong.

Also, we have already stated that y-intercept (c) is where the graph crosses the y-axis or when x = 0.

Therefore, since c = 3, we can further eliminate Option B because it crosses the y-axis at -3 instead of 3.

Finally in order to choose what the answer is between Options A and C, we should substitute

y = 0 into the equation to determine the equation when the graph crosses the x-axis (i.e. when y = 0)

This is done below:

`\begin{gathered} y=(2)/(3)x+3 \\ \text{substitute y= 0} \\ \\ 0=(2)/(3)x+3 \\ \text{subtract 3 from both sides} \\ -3=(2)/(3)x \\ \\ \text{ multiply both sides by}(3)/(2) \\ \\ -3*(3)/(2)=(2)/(3)x*(3)/(2) \\ \\ \therefore x=-(9)/(2)=-4.5 \end{gathered}`

This means that the graph passes through the x-axis at -4.5.

The only option that has this characteristic out of Options A and C is Option C.

Therefore, the final answer is Option C