The slope of a line is given by the formula:

Where m is the slope, (x1,y1) and (x2,y2) are the coordinates of two points on the line.
In the first line we can identify the next two points: (0,0) and (2,1).
The slope of this line is:
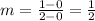
In the second line, the two points that we can identify are: (0,4) and (2,1).
The slope is then:

In order to know if they are perpendicular, we need to know that two perpendicular lines have slopes that are negative reciprocal to each other, it means:
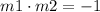
We need to check if this is true with the two slopes we have, then :
![undefined]()