Let x and y be the amounts invested in the one paying 9% and the one paying 10% respectively.
x + y = 14000 ------------------------------------------(1)
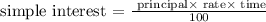
For the one paying 9% simple interest
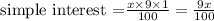
and
for the one paying 10% simple interest
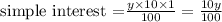
Hence,
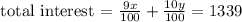
Therefore,
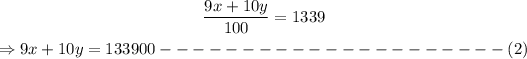
From equation (1), isolating x, we have
x = 14000 - y --------------------------------(3)
Substituting equation (3) into equation (2), we have
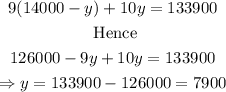
Substituting the y = 7900 into equation (3), we have
x = 14000 - 7900 = 6100
Hence,
he invested $6100 in the account with 9% simple interest
and $7900 in the account with 10% simple interest