Question

For a data set of the pulse rates for a sample of adult females, the lowest pulse rate is 35 beats per minute, the mean of the listed pulse rates is x=75.0 beats per minute, and their standard deviation is s=22.3 beats per minute.

Answer 1

a. 40 beats per minute

b. 1.79 standard deviations away from the mean

c. z = -1.8

d. Yes. The pulse rate of 35 is significant

Step-by-step explanation:

We were given that:

Lowest pulse rate = 35 beats per minute

Mean pulse rate = 75 beats per minute

Standard deviation = 22.3 beats per minute

a. The difference between the Mean pulse rate and lowest pulse rate is given below:

`\begin{gathered} =75-35 \\ =40\text{ }beats\text{ }per\text{ }minute \end{gathered}`

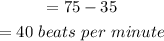
b. The lowest pulse rate is how many standard deviations away from the mean

`\begin{gathered} =(40)/(22.3) \\ =1.79 \end{gathered}`

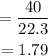
This shows that the lowest pulse rate is 1.79 standard deviations away from the mean

c. The z-score is shown below:

`\begin{gathered} Z=((X-µ))/(σ) \\ X=35 \\ µ=75.0 \\ σ=22.3 \\ \text{Substituting the variables into the formula, we have:} \\ Z=((35-75.0))/(22.3) \\ Z=(-40)/(22.3) \\ Z=-1.7937\approx-1.80 \\ Z=-1.8 \end{gathered}`

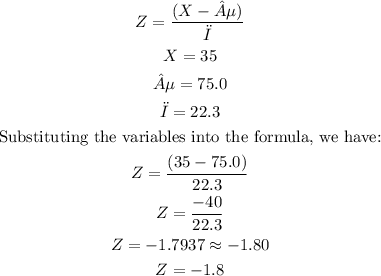
d. If the pulse rates with z-scores between -2 and 2 are neither significantly low nor significantly high, the pulse rate of 35 is significant