A parabola has the following general form:
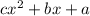
Having a set of (x,y) points like those given by the table one can estimate the value of the parameters a,b and c. In order to do this three equations can be used:
In these equations x and y represent the values given in the table. x is the time t and y is the height h(t). In order to solve these equations first we need to construct a table for the quantities:
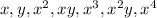
The table is:
The elements of the last row are the ones we are going to use to build the three equations:
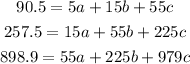
By solving this system of equations we find a, b and c and ith that we will find the approximation we were looking for. So from the first:
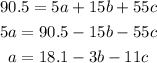
We replace this expression for a in the second equation:
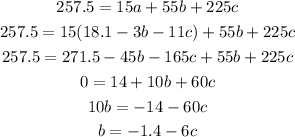
And we replace this expression for b in the expression for a:
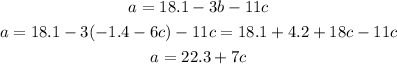
And we replace these expressions for a and b in the third equation:
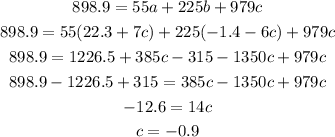
Then we can find a and b:
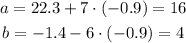
With this results we have that the parabola that approximates the height is:
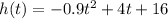
Then, after 6.5 seconds the approximate height is:
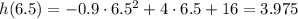
Then the answer is 3.975 ft