Solution:
The distance d between any two points is expressed as
![\begin{gathered} d=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2} \\ \text{where} \\ (x_1,y_1)\text{ and }(x_2,y_2)\text{ are the respective coordinates of the points} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/c09fttzb8ylahm5ya6lyscgmrtnnqx6z17.png)
Given the points labeled A and B as shown below:
step 1: Evaluate the coordinates of A and B.
Thus,
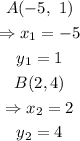
step 2: Evaluate the distance between the points A and B.
![\begin{gathered} d_(AB)=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2} \\ =\sqrt[]{(2-(-5))^2+(4-1)^2} \\ =\sqrt[]{(2+5)^2+(4-1)^2} \\ =\sqrt[]{7^2+3^2} \\ =\sqrt[]{49+9} \\ =\sqrt[]{58} \\ \Rightarrow d_(AB)=7.615773106 \\ \therefore d_(AB)\approx7.6\text{ units (nearest tenth)} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/9o9ftxxknj0a8ioiaclcxko6b6dhyjgczq.png)
Hence, the distance between the points is 7.6 units (nearest tenth).