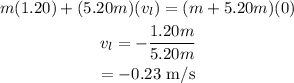Given data
*The given mass of the empty freight car is m_1 = m
*The given initial speed of the empty freight car is v_1 = 1.20 m/s
*The mass of the fully loaded boxcar is m_2 = 5.20 m
*The initial speed of the fully loaded boxcar is v_2 = 0 m/s
(A)
The formula for the speed of the two cars after the collision is given by the conservation of momentum as
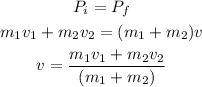
Substitute the known values in the above expression as
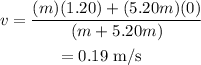
Hence, the speed of the two cars after the collision is v = 0.19 m/s
(B)
As from the given data, the two cars are at rest after the collision. It means the final speed of the two cars equals to zero (v_f = 0 m/s).
The formula for the speed of the loaded box car before the collision is given by the conservation of momentum as
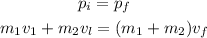
Substitute the known values in the above expression as