to find a perpendicular line to another we need to know the slope of the first line, Fortunately we can find the slope with the two points
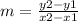
where m is the slope (x2,y2) a point right from (x1,y1)
on this case (x2,y2)=(9,5) and (x1,y1)=(-3,9)
so replacing
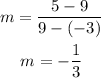
knowing the slope we can find the slope of the perpendicular and this is all than we need to make to lines paralels:
reverse slope and change the sign
so the slope of the new line is 3

to write a equation we can use the general form

where y is the solution, m the slope and x the variable and b it doesnt matter on this case because two lines are only made perpendicular by their slope, so you can use any number
like this
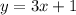
that was the equation