9. What is the length of AB? Explain your reasoning.
Let
A(-5,5)
B(-5,-1)
to find the length you can use the distance between two points formula
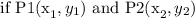
the distance between P1 and P2 is
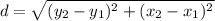
Step 1
put the values into the equation
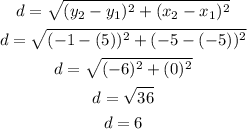
so, the length of AB is 6 units
10. What is the midpoint of CD? Justify your answer.
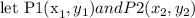
the midpoint of P1 and P2 is
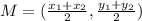
Step 2
Put the values of C and D into the equation
let P1=C and P2=D
C(-3,4) and D(6,3)
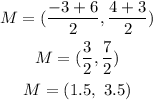
so, the midpoint is (1.5,3.5)
I hope this helps you