Question

A college graduate expects to earn a salary of $50,000 during the first year after graduation and receive a 3% raise every year after that. What is the total income he will have received after ten years? A. $515,000.00 B. $507,955.31 C. $640,389.78 D. $573,193.97 SUBMIT

Answer 1

This problem is an example of a Geometric Progression (GP).

A GP usually has the following parameters to describe it:

`\begin{gathered} a=\text{ First term} \\ r=\text{ Common ratio} \end{gathered}`

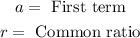
From our question, we have the first term to be 50000, and the common ratio is a 3% increase.

We know that if a percentage (p) is given, the actual ratio is given as

`\begin{gathered} r=(p)/(100)+1\text{ (For increments)} \\ or \\ r=1-(p)/(100)\text{ (for reductions)} \end{gathered}`

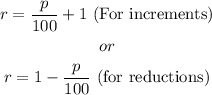
Therefore, the common ratio in our case is

`r=(3)/(100)+1=1.03`

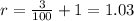
We are to calculate the sum of the GP in the question. The formula for the sum of a GP is given as

`S_n=(a(r^n-1))/(r-1)`

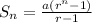
Since we're calculating the total income up to 10 years, we have

`n=10`

Therefore, we can calculate the sum to be

`\begin{gathered} S_(10)=(50000(1.03^(10)-1))/(1.03-1) \\ S_(10)=573193.97 \end{gathered}`

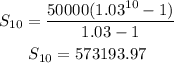
The correct option is OPTION D.