Solution: 24.096
Analysis:
We have a triangle and know two angles and one side of the triangle. According to the angle rule, a triangle's total intern angles equals 180 degrees. We have:
mm∠B=19°
∠A+∠B+∠C=180°
55°+19°+∠C=180°
∠C=180°-55°-19°
∠C=106°
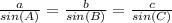
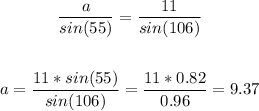
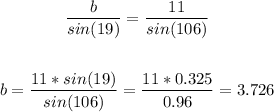
Perimeter=a+b+c
Perimeter=9.37+3.726+11
Perimeter=24.096