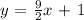Given:
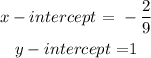
Recall that we can write the intercepts as coordinates:

point-slope form:
The point-slope is defined as :
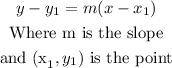
To find the point-slope formula, we use the formula:
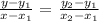
Substituting the given points:
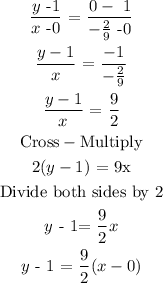
Answer:
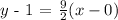
Slope-intercept form
The slope intercept form is defined as:

Using the result from the point-slope form:
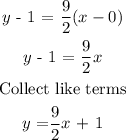
Answer: