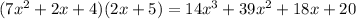Question

I was wondering what is the product of these polynomials
`(7 {x}^(2) + 2x + 4)(2x + 5)`

Answer 1

According to the distributive property, multiplying the sum of two or more addends by a number will give the same result as multiplying each addend individually

`a\cdot(b+c)=a\cdot b+a\cdot c=ab+ac`

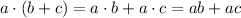
Expanding this concept to the product between sums, we have:

`(a+b)\cdot(c+d)=(a+b)\cdot c+(a+b)\cdot d=ac+bc+ad+bd`

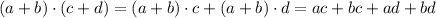
Using this property in our problem, we have:

`\begin{gathered} (7x^2+2x+4)(2x+5) \\ =(7x^2)\cdot(2x)+(2x)\cdot(2x)+(4)\cdot(2x)+(7x^2)\cdot(5)+(2x)\cdot(5)+(4)\cdot(5) \\ =14x^3+4x^2+8x+35x^2+10x+20 \\ =14x^3+39x^2+18x+20 \end{gathered}`

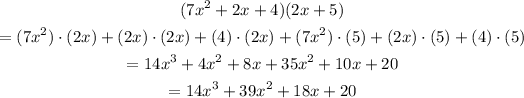
And this is our answer:

`(7x^2+2x+4)(2x+5)=14x^3+39x^2+18x+20`