Question

Find the equation of the line that is parallel to y=x-3 and contains the point that (3,-2)

Answer 1

Given that;

A line is parallel to y=x-3 and contains the point that (3,-2).

To find the equation of the line, the slope-intercept form of a line is

`\begin{gathered} y=mx+c \\ Where\text{ } \\ m\text{ is the slope} \\ c\text{ is the y-intercept} \end{gathered}`

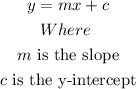
The slope of the given equation is

`\begin{gathered} y=x-3 \\ m=1 \end{gathered}`

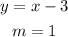
Since the line is parallel to the given equation, the slope of the line is 1

Where

`(x,y)=(3,-2)`

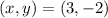
Substitute the coordinates into the slope-intercept form of a line above

`\begin{gathered} y=mx+c \\ -2=1(3)+c \\ -2=3+c \\ Collect\text{ like terms} \\ c=-2-3=-5 \\ c=-5 \end{gathered}`

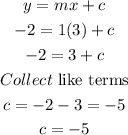
The equation of the line becomes

`\begin{gathered} y=mx+c \\ y=1(x)+(-5) \\ y=x-5 \end{gathered}`

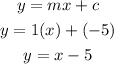
Hence, the answer is

`y=x-5`