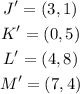Question

4. Square JKLM with vertices J(1, -3), K(5,0),L(8,-4), and M(4, -7): 90° counterclockwiseI'K'(27L'(M' (1-

Answer 1

Given the condition 90 degrees counterclockwise, we use rule below:

When rotating a point 90 degrees counterclockwise about the origin our point A(x,y) becomes A'(-y,x). In other words, switch x and y and make y negative.

Hence, To get J';

`\begin{gathered} A(x,y)=A^(\prime)(-y,x) \\ J(x,y)=J^(\prime)(-y,x) \\ J(1,-3)=J^(\prime)(-(-3),1) \\ J^(\prime)=(3,1) \end{gathered}`

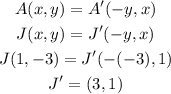
To get K':

`\begin{gathered} K(x,y)=K^(\prime)^{}(-y,x) \\ K(5,0)=K^(\prime)(-0,5) \\ K^(\prime)=(0,5) \end{gathered}`

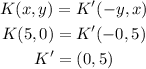
To get L':

`\begin{gathered} L(x,y)=L^(\prime)^{}(-y,x) \\ L(8,-4)=L^(\prime)(-(-4),8) \\ L^(\prime)=(4,8) \end{gathered}`

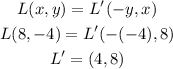
To get M':

`\begin{gathered} M(x,y)=M^(\prime)^{}(-y,x) \\ M(4,-7)=M^(\prime)(-(-7),4) \\ M^(\prime)=(7,4) \end{gathered}`

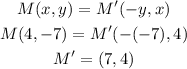
Therefore, the values of J',K',L' and M' are respectively given below;

`\begin{gathered} J^(\prime)=(3,1) \\ K^(\prime)=(0,5) \\ L^(\prime)=(4,8) \\ M^(\prime)=(7,4) \end{gathered}`