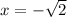Question

Use Second Derivative Test to find minimum and maximum of f(x) =3x^5 - 10x^3

Answer 1

Given the function:

`f(x)=3x^5-10x^3`

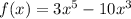
1. You need to find the first derivative.

Remember the Power Rule Derivative:

`(d)/(dx)(x^n)=nx^(n-1)`

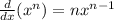
Then:

`f^(\prime)(x)=(3)(5)x^(5-1)-(3)(10)x^(3-1)`
`f^(\prime)(x)=15x^4-30x^2`

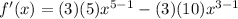
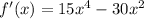
2. Make the first derivative equal to zero:

`15x^4-30x^2=0`

3. Solve for "x":

- Identify the Greatest Common Factor (the largest factor the terms have in common):

`GCF=15x^2`

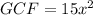
- Factor the Greatest Common Factor out:

`15x^2(x^2-2)=0`

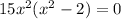
- Notice that you can divide the equation into two parts and solve for "x":

`\begin{gathered} 15x^2=0\Rightarrow x=(15)/(0)\Rightarrow x=0 \\ \\ x^2-2=0\Rightarrow x=\pm√(2)\Rightarrow\begin{cases}x={-√(2)} \\ x={√(2)}\end{cases} \end{gathered}`

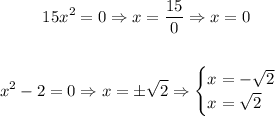
4. Find the second derivate by derivating the first derivative:

`f^{^(\prime)\prime}(x)=(15)(4)x^(4-1)-(30)(2)x^(2-1)`
`f^{^(\prime)\prime}(x)=60x^3-60x^`

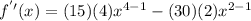
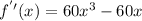
5. Substitute the values of "x" found in Step 3 into the second derivative and evaluate:

`f^{^(\prime)\prime}(0)=60(0)^3-60(0)=0`
`f^{^(\prime)\prime}(-√(2))=60(-√(2))^3-60(-√(2))\approx-84.9`
`f^{^(\prime)\prime}(√(2))=60(√(2))^3-60(√(2))\approx84.9`

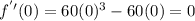
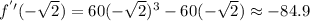
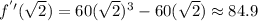
6. According to the Second Derivative Test:

- If:

`f^(\prime)^(\prime)(x)>0`

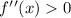
Then the function has a local minimum at that x-value.

- If:

`f^(\prime\prime)(x)<0`

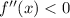
Then the function has a local maximum at that x-value.

In this case:

`f(-√(2))<0`
`f(√(2))>0`

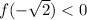
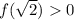
Hence, the answer is:

- Local Minimum at:

`x=√(2)`

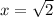
- Local Maximum at:

`x=-√(2)`