We are given the following quadratic inequality

Let us first convert it into quadratic form and then factorize the inequality

Now we need two numbers such that their sum is 6 and their product is -16
How about 8 and -2?
Sum = 8 - 2 = 6
Product = 8*-2 = 16
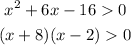
Now there are a few cases possible,
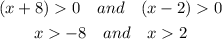
Since x > 2 meets the requirement of x > -8 so we take x > 2 from here.
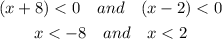
Since x < -8 meets the requirement of x < 2 so we take x < -8 from here.
Therefore, the solution of the quadratic inequality is
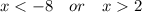
The endpoints are x = -8 and x = 2 (option A is correct)