In the triangle ABC, D and E are the mid point of the sides AB and AC respectively.
Using mid point theorem the line DE is parallel to the side BC, hence triangle
ADE is similar to the ABC.
The side of the similar triangles are proportional,
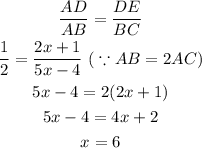
The length of BC can be determined as,
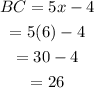
Thus, the required value of side BC is 26.