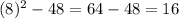WE are given the following
We are told that AE is 16 and that E is the cneter of the parallelogram. The center of the parallelogram has the property that it splits each diagonal into two line segment with the same length. We are told that the length of segment BE is x²-48 and the length of ED is 2x. Thus, we have the following equation
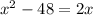
which is equivalent to
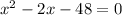
Note that given the polynomial of the form
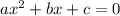
we have that the solutions would be
![x=\frac{-b\pm\sqrt[]{b^(2)\text{ -4ac}}_{}}{2a}](https://img.qammunity.org/2023/formulas/mathematics/college/5jtlron943z4gtdutgnwua7jtwea0nsj60.png)
In our case, we have a=1, b=-2 and c=-48. Thus The solutions would be
![x=\frac{-(-2)\pm\sqrt[]{(-2)^2-4\cdot(-48)}_{}}{2}=\frac{2\pm\sqrt[]{4+192}}{2}=\frac{2\pm\sqrt[]{196}}{2}=(2\pm14)/(2)](https://img.qammunity.org/2023/formulas/mathematics/college/9zi9h15gpi5g8uj39dyea36mui1d6qeker.png)
So the solutions would be
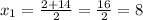
and
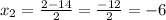
Since DE has length 2x and this number should be positive, we must have that x=8. So, the length of DE would be
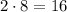
and thus, the distance BE is