SOLUTION
From the given data the mean is 62 and standard deviation is 4
It is required to find the probability that a data value is between 57 and 62
That is:
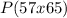
The z scores is calculated using:
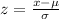
Using the x values it follows:
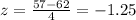
Also,
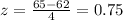
Thus the required probability is:
![P(-1.25The proability is:[tex]P(-1.25This can be expressed as percentage as:[tex]P(-1.25\lt z\lt0.75)=66.8\%](https://img.qammunity.org/2023/formulas/mathematics/college/ujpz5gvt84hvo1yfss1tpzrf3it79jmuwd.png)
Therefore the correct option is C