Explanation
Given information
The following equation was given in the question provided
4x + 5y = 20
To graph the above equation, we need to find the x and y-intercepts of the equation.
To find the x-intercept of the equation, we need to make y = 0
Therefore, we have
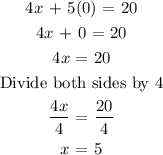
Hence, the x-intercept is (5, 0)
The next step is to find the y-intercept
To find the y-intercept, we need to make x = 0
Then, we have
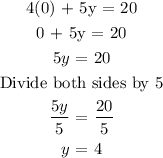
Therefore, the y-intercept is (0, 4)
Since we have gotten the intercepts to be (5, 0) and (0, 4), then, the next process is to graph the intercepts