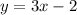SOLUTION
From the line
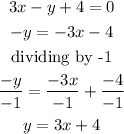
Equation of the line parallel to this line must have the same slope of the line.
From equation of a line in slope-intercept form,
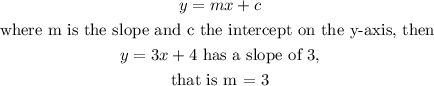
Now, let the new line have the equation
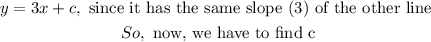
From the function
![\begin{gathered} f(x)=x^3 \\ f^(\prime)(x)=3x^2 \\ To\text{ be tangent to the line }y=3x+c,\text{ the curve should have same } \\ \text{slope and be equal to the line, hence } \\ 3x^2=3 \\ x^2=1 \\ x=\sqrt[]{1} \\ x=1 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/bigchig5ik73y6m4q6rlv9v9szdozc2q22.png)
Substituting the value of x into f(x), we have

So, they are both tangent at (1, 1).
From the equation above we have
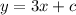
Substituting the values of x = 1 and y = 1 in the above equation, we have
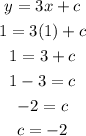
Substituting the c for -2 back into the original equation we have
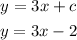
Hence the answer is