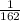Given:
Numbers in the spinner = 1 to 9 ==> 9 numbers
Possibilities in a coin == Head and tail
Given that you spin the spinner flip a coin then spin the spinner again, let's find the probability of spinning a 4, flipping head, then spinning a 7.
We have the following:
• Probability of spinning a 4:
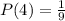
• Probability of flipping head:
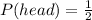
• Probability of spinning a 7:
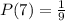
Hence, we have:
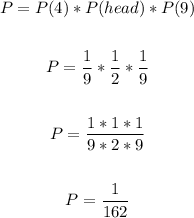
Therefore, the probability is:
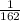
ANSWER: