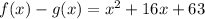Question

given that f (x) = x squared + 17x + 72 and g(x) = x + 9 find f (x)-g (x)and express the result in standard form

Answer 1

Given the functions:

`f(x)=x^2+17x+72`
`g(x)=x+9`

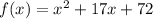
You have to subtract the functions:

`f(x)-g(x)`
`(x^2+17x+72)-(x+9)`

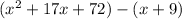
Note that I wrote both functions in parentheses separated by the minus sign. For the seconf term, the minus sign is as if the parenthesis is being multiplied by -1, the sign of both x and 9 is inverted:

`x^2+17x+72-x-9`

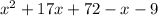
Order the like terms

`x^2+17x-x+72-9`

And simplify

`x^2+16x+63`

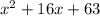
So the result in standard form is

`f(x)-g(x)=x^2+16x+63`