We need to calculate a system of equations using the general formula of the circle
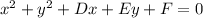
for the point (-5, 5)
x=-5
y=5
the first equation is
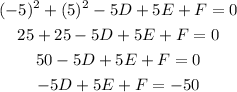
for the point (-5,-3)
x=-5
y=-3
the second equation is
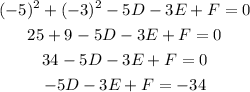
for the point (7, -3)
x=7
y=-3
the third equation is
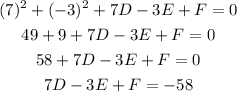
Then we solve the system of equations, and we obtain
D=-2
E=-2
F=50
The equation of the circle that passes through these points is
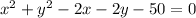
for calculate the coordinates of the center of the circle we have
D=-2h
h is the x coordinate of the center of the circle
D=-2
we isolate the h
h=-2/-2=1
E=-2k
k is the y coordinate of the center of the circle
E=-2
we isolate the k
k=-2/-2=1
the center of the circle is (h,k)=(1,1)