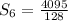Given the series:
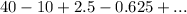
You need to remember that a Geometric Series has a Common Ratio, which is the factor between the terms.
In this case, the series is geometric, because every term is found by multiplying the previous one by:
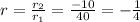
By definition, the sum of the first "n" terms of Geometric Series, can be calculated by using the following formula:
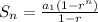
Where:
-The first term is:
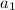
- The number of terms is "n".
- And "r" is the Common Ratio. This must be:
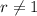
In this case, you can identify that:
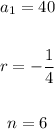
Therefore, substituting values into the formula and evaluating, you get:
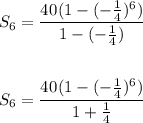
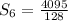
Hence, the answer is: