Question

I have added the question as an image. I don't understnad part (b) of the question.I tried it but got t=2(v0)/g with v0 the intial speed. the answer is: t = v0/gThanks in advance!

Answer 1

Given data

*The intial horizontal velocity of the potato is u_x = v_o

*The vertical acceleration of the potato is a_y = -g

*The given angle is 45 degree

(a)

The formula to calculate the horizontal co-ordinate of potato is given as

`x=u_xt+(1)/(2)a_xt^2`

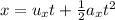
*Here a_x = 0 m/s^2 is the horizontal acceleration of the potato

Substitute the known values in the above expression as

`\begin{gathered} x=v_0t+(1)/(2)(0)(t^2) \\ =v_0t \end{gathered}`

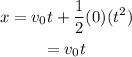
The formula to calculate the vertical co-ordinate of potato is given as

`y=u_yt+(1)/(2)a_yt^2`

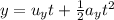
*Here u_y = 0 m/s is the initial vertical velocity of the potato

Substitute the known values in the above expression as

`\begin{gathered} y=(0)(t)+(1)/(2)(-g)t^2 \\ =-(1)/(2)gt^2 \end{gathered}`

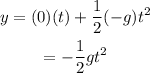
As from the given data, apply the condition as

`\begin{gathered} x=y \\ v_0t=(1)/(2)gt^2 \\ t=(2v_0)/(g) \end{gathered}`

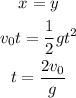
Hence, the equation for the time taken is t = 2v_0/g

The horizontal co-ordinate of potato is calculated as

`\begin{gathered} x=v_0t \\ =v_0((2v_0)/(g))_{} \\ =(2v^2_0)/(g) \end{gathered}`

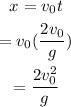
The vertical coordinate of the potato is calculated as

`\begin{gathered} y=-(1)/(2)gt^2 \\ =-(1)/(2)g((2v_0)/(g))^2 \\ =-(2v^2_0)/(g) \end{gathered}`

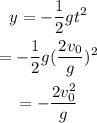
Hence, the co-ordinate of the potato is (2v_0^2/g, -2v_0^2/g)

(b)

The formula to calculate the angle of position co-ordinates is given as

`\tan \theta=(y)/(x)`

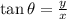
Substitute the known values in the above expression as

`\begin{gathered} \tan 45^0=(y)/(x) \\ x=y \end{gathered}`

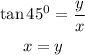
The above equation shows that time taken is the same for the angle and co-ordinate is also the same.

Thus, the equation for the time taken is the same as t = 2v_0/g, and the co-ordinate of the potato is the same as (2v_0^2/g, -2v_0^2/g)