The values of t are 1.42 or 0.70
Step-by-step explanation:
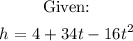
To find the values of t for which height is 20 feet,, we will substitute 20 for h in the equation above:

Next we will solve for t:
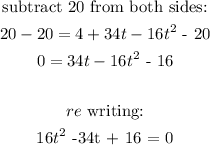
Since we can't easily ascertain if it is factorisable using factorisation method, we will use the formula method to factorise it:
![x\text{ = }\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}](https://img.qammunity.org/2023/formulas/mathematics/college/g6chm4j4qtch7yszwcwrt6mnkvwotsyyab.png)
![\begin{gathered} \text{where a = }16,\text{ b = -34, c = 16} \\ x\text{ = }\frac{-(-34)\pm\sqrt[]{(-34)^2-4(16)(16)}}{2(16)} \\ x\text{ = }\frac{34\pm\sqrt[]{1156-1024}}{32} \\ x\text{ = }\frac{34\pm\sqrt[]{132}}{32} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/6e4fzhm62dz72bdu3ootk27kbdxdwdit66.png)
![\begin{gathered} x\text{ = }\frac{34\pm\sqrt[]{4*33}}{32} \\ x\text{ = }\frac{34\pm2\sqrt[]{33}}{32} \\ x\text{ = }\frac{2(17\pm\sqrt[]{33})\text{ }}{32}=\text{ }\frac{(17\pm\sqrt[]{33})\text{ }}{16} \\ x\text{ = }\frac{17+\sqrt[]{33}}{16}\text{ or }\frac{17-\sqrt[]{33}}{16} \\ x\text{ = 1.42 or }0.70 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/2awgecgknt0bwydtz3i2p07bkmw87npb8n.png)
The values of t to the nearest hundredth are 1.42 or 0.70