For part A, the only possible option that could represent a rational number is
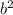
Because all the other options are irrational numbers.
For part B, the other zero has to be irrational too. To prove this we use the general formula for quadratic equations:
![\begin{gathered} x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \\ \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/nk3bft20xor7rzbiz28ysgt23i1xfm7d29.png)
If x1 is an irrational number, then
![\sqrt[]{b^2-4ac}\text{ }](https://img.qammunity.org/2023/formulas/mathematics/college/rwfwivm51hnm10l218u1vs995bcshu4n31.png)