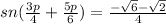Question

I need help on 23 all i know is the formula: sin(a+b)=((sin(a))(cos(b)))+((cos(a))(sin(b)))

Answer 1

N 23

we have

`sin((3pi)/(4)+(5pi)/(6))`

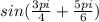
Remember that

`sin\left(a+b\right)=sin\left(a\right)cos\left(b\right)+cos\left(a\right)\lparen sin\left(b\right)`

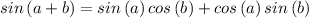
substitute given values

Remember that

3pi/4=135 degrees ------> reference angle is 45 degrees

135 degrees -----> II quadrant ----> sine is positive and cosine is negative

so

sin(3pi/4)=sin(45)=√2/2

cos(3pi/4)=-cos(45)=-√2/2

5pi/6=150 degrees ----> reference angle is 30 degrees

150 degrees -----> II quadrant -----> sine is positive and cosine is negative

sin(5pi/6)=sin(30)=1/2

cos(5pi/6)=-cos(30)=-√3/2

Substitute the given values in the formula

`s\imaginaryI n((3p\imaginaryI)/(4)+(5p\imaginaryI)/(6))=(√(2))/(2)*(-(√(3))/(2))+(-(√(2))/(2))*((1)/(2))`
`s\imaginaryI n((3p\imaginaryI)/(4)+(5p\imaginaryI)/(6))=-(√(6))/(4)-(√(2))/(4))`

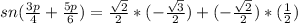
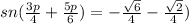
The answer is

`s\imaginaryI n((3p\imaginaryI)/(4)+(5p\imaginaryI)/(6))=(-√(6)-√(2))/(4)`