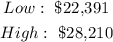Part a.
From the given information, we have that
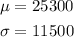
Then, the distribution of X
is given by:
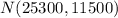
Part b.
In this case, we need to find the following probability:
![P(22600then we need to find the corresponding z values for there values, that is, [tex]z=(22600-25300)/(11500)=-0.23478](https://img.qammunity.org/2023/formulas/mathematics/college/g0zw35ir1lfbjq4006x9u8ayw7odj26fsi.png)
and
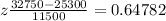
So we need to find on the z-table the following probability:
![P(-0.23478which gives 0.33426<p>Therefore, by rounding to 4 decimal places, <strong>the answer for part b is: 0.3343.</strong></p><p>Part c.</p><p>The middle 20% of college graduate loans debt lies within the interval 10% below the mean and 10% over the mean. Then, the z-value for this interval is z=+/- 0.253</p><p></p><p>Then, we can find the lower and upper bound for this interval as</p>[tex]\begin{gathered} Lower=\mu-z*\sigma=25300-0.253*11500 \\ Upper=\mu+z\sigma=25,300+0.253*11,500 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/yvhrb8fqqw1mjjibmu8s1n8u7sb6mnle4b.png)
which gives
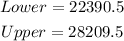
Therefore, by rounding up to the neares dollar, the answers for part c are: