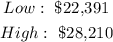Question

The average student loan debt for college graduates is $25,300. Suppose that that distribution is normal and that the standard deviation is $11,500. Let X = the student loan debt of a randomly selected college graduate. Round all probabilities to 4 decimal places and all dollar answers to the nearest dollar.a. What is the distribution of X? X ~ N(,)b Find the probability that the college graduate has between $22,600 and $32,750 in student loan debt. c. The middle 20% of college graduates' loan debt lies between what two numbers? Low: $ High: $

Answer 1

Part a.

From the given information, we have that

`\begin{gathered} \mu=25300 \\ \sigma=11500 \end{gathered}`

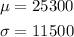
Then, the distribution of X

`N(\mu,\sigma)`

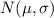
is given by:

`N(25300,11500)`

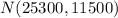
Part b.

In this case, we need to find the following probability:

`P(22600then we need to find the corresponding z values for there values, that is, [tex]z=(22600-25300)/(11500)=-0.23478`

and

`z(32750-25300)/(11500)=0.64782`

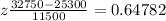
So we need to find on the z-table the following probability:

`P(-0.23478which gives 0.33426<p>Therefore, by rounding to 4 decimal places, <strong>the answer for part b is: 0.3343.</strong></p><p>Part c.</p><p>The middle 20% of college graduate loans debt lies within the interval 10% below the mean and 10% over the mean. Then, the z-value for this interval is z=+/- 0.253</p><p></p><p>Then, we can find the lower and upper bound for this interval as</p>[tex]\begin{gathered} Lower=\mu-z*\sigma=25300-0.253*11500 \\ Upper=\mu+z\sigma=25,300+0.253*11,500 \end{gathered}`

which gives

`\begin{gathered} Lower=22390.5 \\ Upper=28209.5 \end{gathered}`

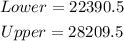
Therefore, by rounding up to the neares dollar, the answers for part c are:

`\begin{gathered} Low:\text{ \$22,391} \\ High:\text{ \$28,210} \end{gathered}`